20.1 Statistische Auswertung über den arithmetischen Mittelwert
Bei der statistischen Auswertung der Ergebnisse von Betonprüfungen werden in der Regel der arithmetische Mittelwert x, die Standardabweichung s und der Variationskoeffzient V als Maß für die Streuung bestimmt.
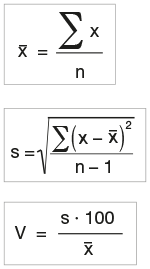
|
mit |
x – arithmetischer Mittelwert der Prüfergebnisse |
| x – einzelne Prüfergebnisse | |
| n – Anzahl der Prüfergebnisse | |
| s - Standardabweichung | |
| V - Variationskoeffizient |
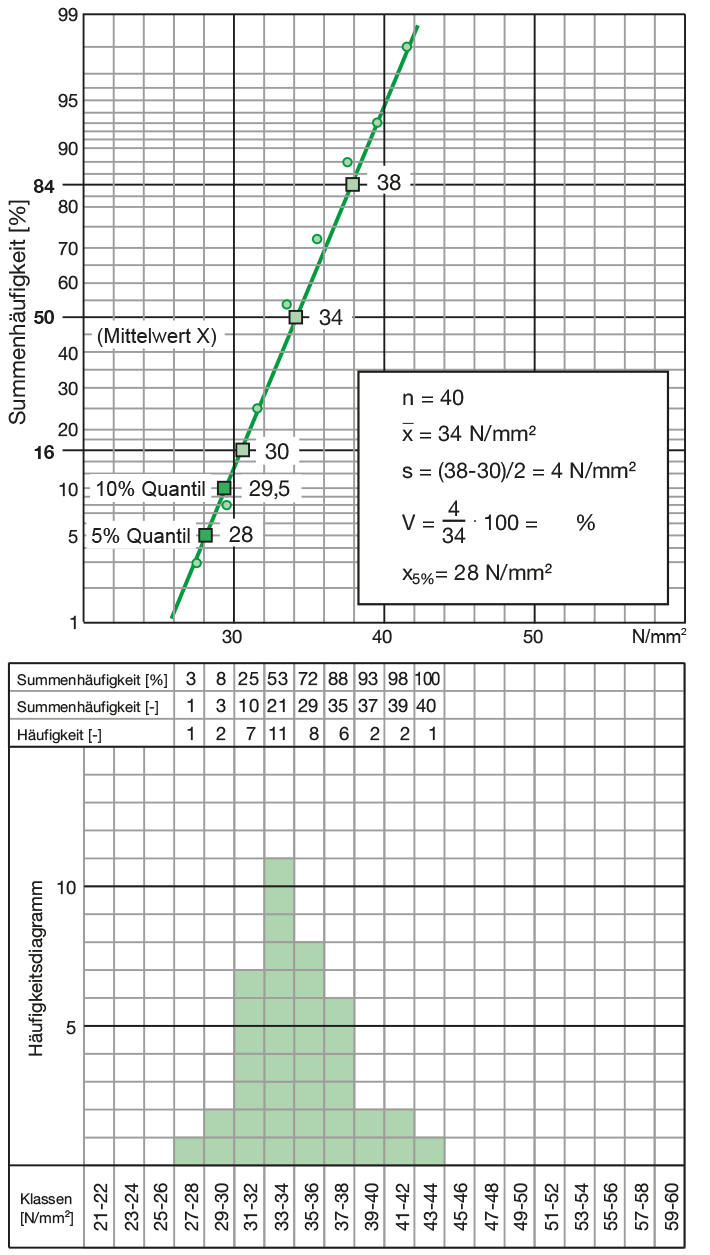
Die Auswertung, z. B. für Betondruckfestigkeitsergebnisse, kann auch zeichnerisch wie folgt durchgeführt werden (siehe nachfolgende Abbildung):
- Die Prüfergebnisse werden in Klassen eingeteilt und in ein Häufigkeitsdiagramm eingetragen. Jeder Eintrag entspricht einem Prüfergebnis.
- Die Einträge werden innerhalb jeder Klasse gezählt und ihre Anzahl in der Zeile „Häufgkeit“ eingetragen.
- Die Summenhäufigkeit wird von links beginnend bestimmt.
- Die prozentuale Summenhäufigkeit wird berechnet. Diese Werte werden in das Wahrscheinlichkeitsnetz (Normalverteilung) eingetragen und es wird eine Ausgleichs-Gerade gezogen.
- Der Mittelwert x wird an der 50 %-Linie abgelesen abgelesen.
- Die Standardabweichung s (Gesamtstreuung) ist die halbe Differenz der Festigkeiten bei 16 % und 84 % Summenhäufigkeit. Im Bereich x ± s liegen etwa zwei Drittel aller vorkommenden Prüfwerte.
- Die 5 %- bzw. 10 %-Linie (5 %- bzw. 10 % Quantil) im Wahrscheinlichkeitsnetz gibt die Grenze an, die von höchstens 5 % bzw. 10 % der Prüfwerte unterschritten wird.
Im Fall einer Normalverteilung gilt annäherungsweise:
- Mittelwert x ± Standardabweichung (s): 68 % aller (Mess-)Werte sind erfasst
- Mittelwert x ± 2fache Standardabweichung (2 s): 95 % aller (Mess-)Werte sind erfasst
- Mittelwert x ± 3fache Standardabweichung (3s): 99 % aller (Mess-)Werte sind erfasst
Beispiel einer Festigkeitsauswertung - Wahrscheinlichkeitsnetz